Training Tiny LLMs to Play Connections Better than Frontier Models

This blog post has no relation to my work, and is simply a personal project for my own entertainment. It's also quite old - I started working on this late last year, but life happens and I only got around to evaluating writing it up recently.

Amid the fervor for DeepSeek R1's release, and after watching extensive experimentation on Twitter around training tiny reasoning models for various tasks with verifiable rewards, I decided to join the fun. I'd also been wanting to write something similar to nanoGPT for RL with verifiable rewards, and needed a task that could serve as a test bed for experimenting with different RL algorithms.

Math and coding puzzles had already been done (and that's too close to my day job anyway); what else was worth trying? As I started thinking through the options, a few criteria became clear:

• The task should be something that a very small language model (1B params) is already capable of doing somewhat reliably. This ensures that the reward returned is nonzero at least once, ideally more, per group of completions. If the model can't succeed at all initially, it has no signal to learn from.
• The reward needs to be reasonably dense. One early option I considered was Twenty Questions - it seemed like a good fit, as it requires wide-ranging world knowledge and can vary widely in difficulty. However, in that game, you either win or lose the entire game at once; there is no score assigned at each question asked. While variable reward could be given based on the number of guesses required (with another LLM as the validator), if the model isn't smart enough to win sometimes, it'll never learn how to win at all.
• Ideally, the task gives some sort of score at each step, ensuring few or no batches with all rewards of 0. With GRPO, there is no value estimate - advantage is calculated via the final reward - so gradients are smaller if the standard deviation of rewards in a group is lower. Conversely, more variance leads to larger gradients and (hopefully) faster learning.

So what games work well out of the box? In this regard I was lucky: my girlfriend and I have been playing NYT's Connections for a long time, and one day I realized that the game provides exactly the kind of dense, partial reward I was looking for. I wrote out a quick rubric:

• For a submission, check the number of groups submitted; it should be exactly four.
• For each group, the number of words should also be exactly four.
• Within each group, score the number of words that match a group in the ground truth.

Next, I needed to parse the results for verification. I went with a standard tag-based format:

<answer>  
<group> jonas, marx, warner, bass </group>  
<group> bassoon, harp, recorder, absurdity</group>  
<group> folly, madness, nonsense, sen </group>  
</answer>

For a dataset, there were several approaches to consider:

• Using the NYT's archive was out of the question due to copyright, and several other projects had been struck down for using community-sourced archives of previous solutions.
• I could have an LLM generate groups of 4 related words, then randomly group them together. However, the difficulty in Connections comes from words having double meanings, making it non-obvious which group a word belongs to.
• I could generate 4 groups at once in a single pass. I tried this, and while it worked, it had issues. Often the groups would be too easy, or the model would break the rules, generating a group of 5 words or fewer than 4 groups. (Even recent reasoning models struggled with this!)

I finally landed on generating 2 groups of 4 words, then randomly merging 2 of these groups together. This hit a sweet spot in terms of difficulty and the LLM's ability to follow instructions. My belief is that models are good at understanding double meanings but can get stuck when given too large a space of possible words. I also generated a list of seed words (all simple nouns) and instructed the model to use at least one seed word - this improved diversity significantly.

Once I had a dataset, I needed an algorithm and reward function. I started with REINFORCE, then switched to GRPO; in my experiments, GRPO converged more quickly, though both options were fairly stable and produced similar train/test reward scores. For the reward function, I started simple: out of all the correct groupings, how many would the model get in a single-shot setting?

The immediate results with a 7B model were surprisingly good - in fact, the model performed so well even within the first ~100 steps that it would get all groupings correct, leading to batches with 0 standard deviation and thus 0 gradient. So I needed to make the questions harder - but this is easier said than done. A good Connections puzzle requires finding 16 words with enough inter-word relationships that the correct groupings aren't obvious, but not so many that the puzzle becomes impossibly difficult. (Even official NYT puzzles can hit these extremes sometimes.) I dramatically increased the number of combinations from ~1k to 10k by simply sampling more combinations and generating more data.

This allowed training to progress, though it was still fairly slow and prone to collapse if I tweaked hyperparameters much. I added partial rewards - instead of requiring all 4 groups to be correct, I'd reward getting n/4 groups correct. From viewing online generations, I noticed the model tended to generate too many groups or hallucinate words not in the prompt. I began penalizing each of these minor failure modes, but it turned out that simply adding examples of the output format did a better job of keeping the model on track. Anything we can avoid having the model learn during the online RL phase, we should.

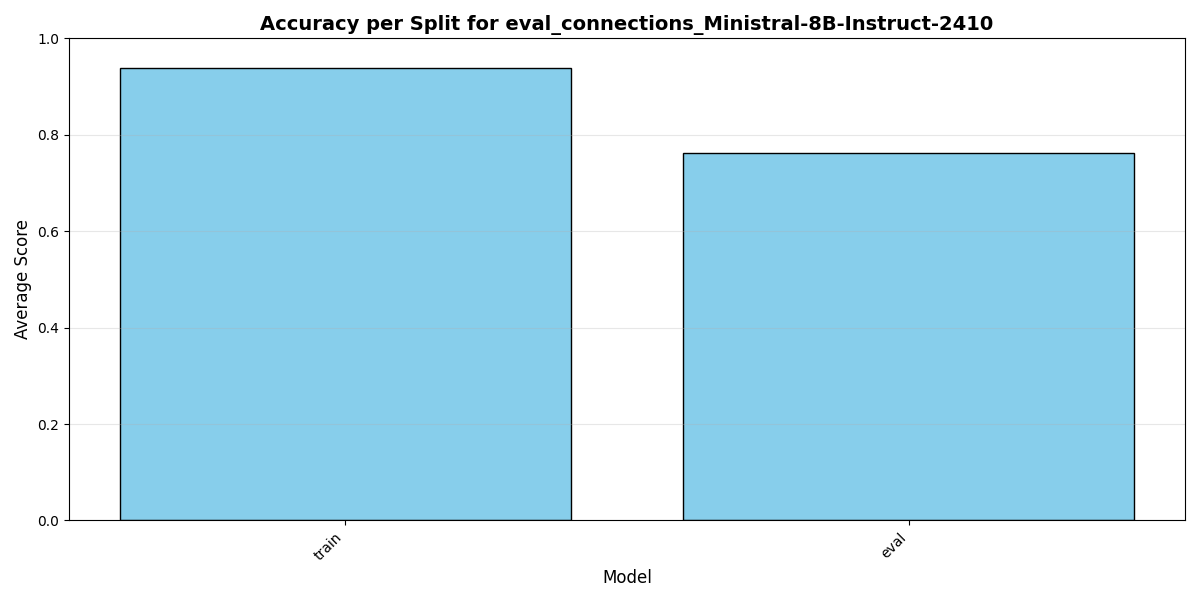The initial benchmark results from the first trained checkpoint.

After reaching a good baseline - where reward saturated and evals showed results within ~10% on my holdout set - I wondered if I could reduce the base model size and still get good results. So I chose a much smaller model - the 500m parameter Qwen-3 variant - and started trying things.

Another technique I explored was hyperparameter scheduling. I see this as performing a role similar to epsilon-greedy - as the model learns to select actions more effectively, we want to increase the chance that it'll explore parts of the state space it hasn't seen before. In the case of an LLM, however, we also need to adjust the task given to the model, as we're conditioning the 'environment' (the tokens generated during inference) on said task. To that end, I added a temperature schedule based on the current reward standard deviation - increasing temperature as std decreases - and also recorded the difficulty of the current steps (i.e., the average reward) so that we could re-use those samples as needed later in the training process. With these tricks, we're able to solidly beat both the 7B model and a good number of frontier offerings.

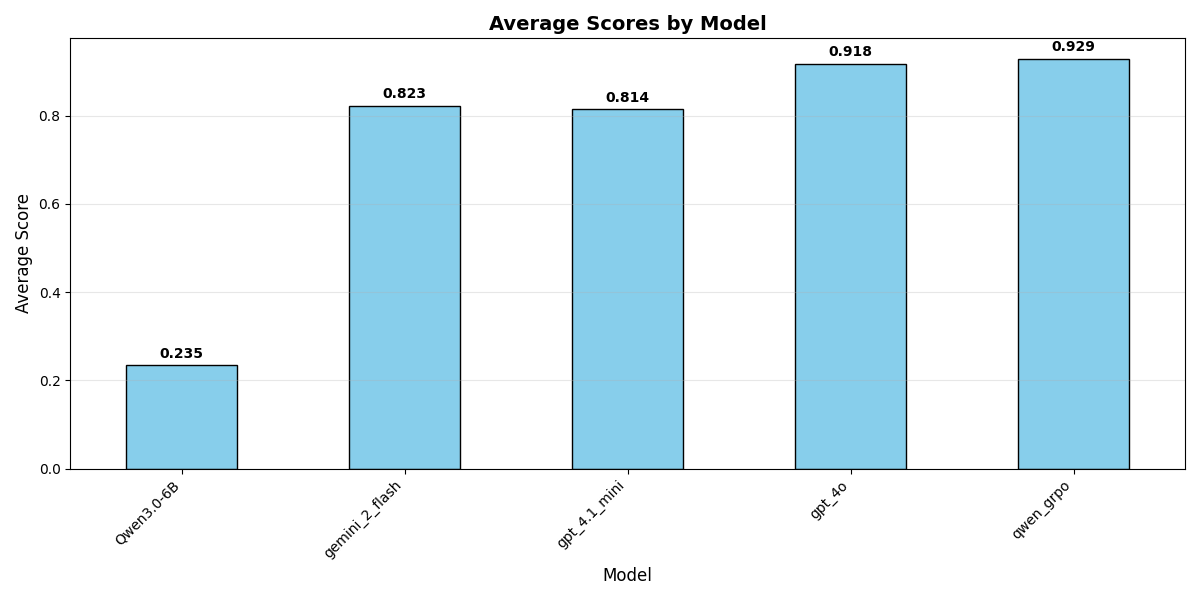
The benchmark results from the last, optimized model, versus frontier models at the time of writing.

I was impressed by how far these small LMs can be pushed on tasks that are considered difficult for frontier models, with careful application of RL. I learned a lot working on this, and I'm excited to see what other capabilities are hidden within smaller models, waiting to be revealed.

The code for this project is available on GitHub here, and the fine-tuned checkpoint is up on HuggingFace here. I'm happy to provide eval results and datasets upon request.