Reviewing Post-Training Techniques from Recent Open LLMs

Whenever a new technical report is released for an open LLM, I like to give it a skim to see if there are any novel post-training techniques, as that's what I've been working on lately. When these techniques are used in large-scale models available to the public, it's more convincing to me than when it's demonstrated in a standalone paper or a small-scale model. This post is a roundup of some of the techniques I've seen in recent reports, and a brief overview of how they work.

Unfortunately, none of these model reports contain ablation metrics for the techniques reviewed; at their scale, it might have been prohibitively expensive to do so, but this does leave the question open as to how effective these techniques are in isolation¹. I'll also be skipping details not related to post-training techniques, so this won't be a full paper review; I'd suggest checking Sebastian Raschka's blog for more in-depth reviews of papers in that vein.

Pivotal Token Search (Phi-4)

Paper link

Detailed in section 4 of the Phi-4 paper, pivotal token search is a variant of DPO that accounts for the fact that there are often specific tokens in a completion that can cause a model to derail from a correct answer, in verifiable use cases such as code generation or math reasoning. The paper proposes that for each token, you can determine an incremental increase in the conditional probability of success of the entire completion for that token; if this is applied to the entire completion, you would find certain 'pivotal' tokens in the completion that radically increase or decrease the probability of completion success. They also note that tokens with a low probability in the chosen completion could potentially contribute positively to the loss, even if it massively reduces the likelihood of completion success.

Figure 3 from the Phi-4 paper. The chart at the bottom shows the probability of success for an independent completion starting at that token index.

Given a list of pivotal tokens, we could in theory generate preference data that focuses on just completions from those pivotal tokens, teaching the model to make the right decisions in those cases. The process the paper suggests for doing this goes like this:

1. Perform a binary search by recursively splitting a sequence into segments.
2. At each split, calculate $p_{success}$ as the conditional probability of success of the completion given that sequence as a prefix, verified with an external oracle (i.e., comparing with the correct answer in a math question, or running the unit tests in a code generation task).
3. If the difference in probability of success between the token and the token plus the next token is greater than a threshold, output the token as a pivotal token, and continue to split the sequence.

Here's a Python implementation of this process, interpreted from the algorithm listed in the paper:

def pivotal_token_search(Q: str, T_full: str, p_gap: float) -> Iterator[Tuple[str, str, str]]:
    def subdivide(T_prefix: str, T: str) -> List[str]:
        # Check if the difference in probability of success is less than the threshold;
        # if so, this cannot be a pivotal token, so return as base case.
        if len(T) <= 1 or abs(p_success(Q, T_prefix) - p_success(Q, T_prefix + T)) < p_gap:
            return [T]

        # Split at the cumulative midpoint of token log probabilities
        T_left, T_right = split(T)

        # Recursively subdivide.
        # In an efficient implementation, we would cache the results of each subdivide.
        return subdivide(T_prefix, T_left) + subdivide(T_prefix + T_left, T_right)

    T_prefix: str = ""
    # Iterate over all tokens returned by subdivide
    for T in subdivide("", T_full):
        if len(T) == 1 and abs(p_success(Q, T_prefix) - p_success(Q, T_prefix + T)) >= p_gap:
            # Output pivotal tokens T and context for postprocessing
            yield Q, T_prefix, T
        T_prefix += T

The paper notes that this is an expensive process, but we can reuse the KV cache from the language model, and memoize the results of the binary search to make it more efficient.

An example of a completion from PTS. Note how the positive and negative completions are totally differently worded.

I'm excited about this technique as most of the 'reasoning' research focuses on more expensive RL techniques like PPO, whereas DPO is much cheaper, making it more accessible; this also seems to be a clever way to work around DPO's lack of fine-grained credit assignment, which is a common criticism of the technique. I'm hopeful we see more research on the topic of applying DPO to reasoning, as Step-Controlled DPO or Step-DPO show that there's a lot of potential.

GRPO (DeepSeek Math & DeepSeek V3)

Paper link

While this technique first gained wide attention in the DeepSeek-v3 report, GRPO was first defined in the report for DeepSeek Math, released in April '24. DeepSeek-Math was trained from DeepSeek-Code 7b, with the goal of SOTA performance on math and math reasoning tasks. The general outline for their training process was:

1. Perform pretraining on a math-specific corpus of 120B tokens.
2. Perform SFT on high-quality math samples, with an instruct template, which introduces a conversation format as well as improved performance on structured math problems.
3. Finally, perform RLHF with math-specific samples.

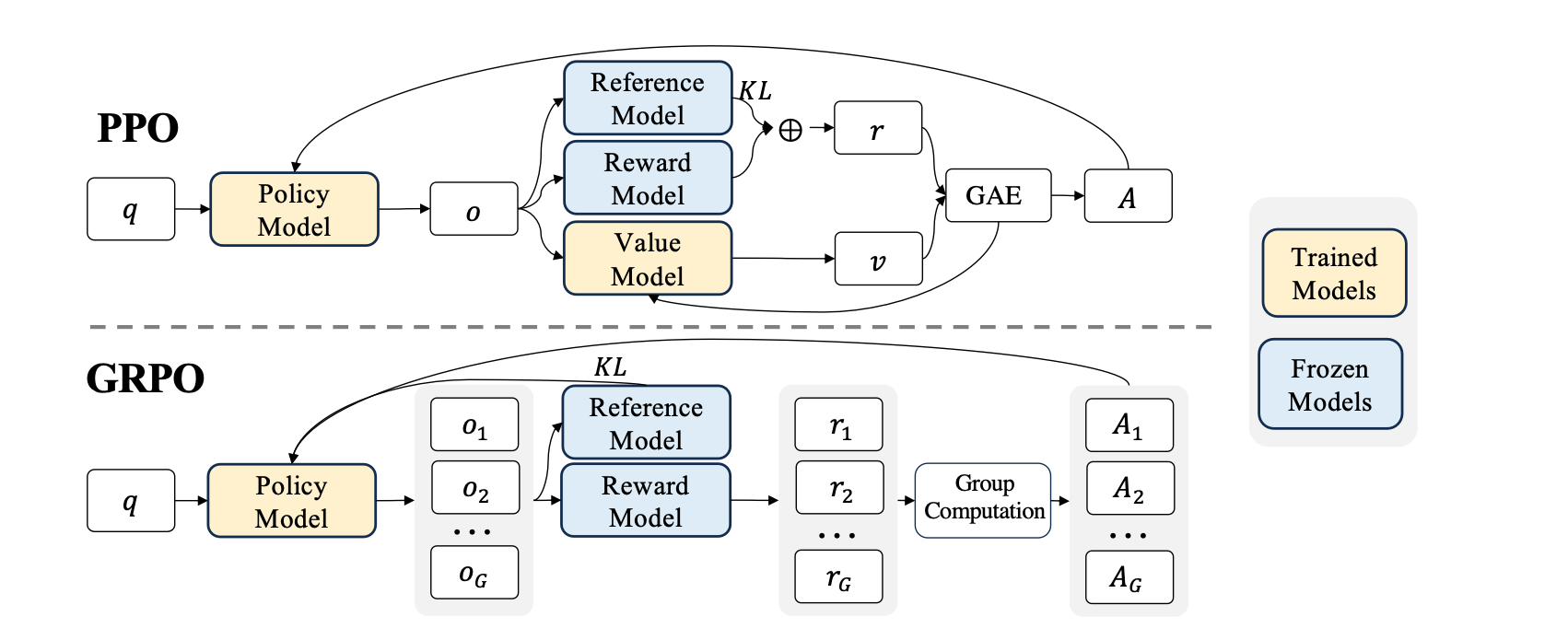
This third step is where GRPO is introduced; it's a variant of the commonly-used PPO algorithm, which, when used with RLHF in the original formulation, requires 4 models to be loaded:

1. The reference model (aka a frozen copy of the base model).
2. The policy model (the model that is being trained).
3. The reward model (for calculating the reward signal).
4. The value model (for calculating the value of each action, per step). This is often similar in architecture to the reward model, or in some cases a separate head on the reward model.

Clearly, this is pretty expensive, and can be extremely difficult to scale; since on-policy generation is part of the training process, efficient sampling with these same models is required, and so you end up with lots of sync points and a lot of different services that have to scale differently.

While GRPO still requires a reference, policy and reward model, it removes the need for a value model. Instead, it uses the average reward of multiple sampled outputs to the same input as the baseline. This also has the benefit of simplifying the advantage calculation for variance reduction; value training can be unstable, so having a more stable baseline can be beneficial as well.

GRPO is used with a process reward model, as well as an outcome reward model, in DeepSeek Math, which calculates the reward from the score given for each step of the reasoning process. In this formulation, the advantage of each token can simply be calculated as the normalized sum of rewards from all following steps, i.e.:

$$A_{i, t} = \text{index}(j) \geq t \, r_{\text{index}(j)}$$

This avoids a few other issues with process-based rewards and RLHF - namely, that a value estimate at each step can give totally unstable and unreliable estimates compared to the actual reward, and that the reward signal can be very sparse, making it difficult to train a value model for reasoning use cases. I'd be very interested to see how this compares in a side-by-side comparison with the original PPO formulation, as well as how it performs in other reasoning tasks.

Online Merging Optimizer (Qwen-2)

Qwen 2 paper

Online Merging Optimizer paper

Online Merging Optimizer source code

Qwen-2 is an LLM trained by Alibaba, with open weights, that performed competitively with GPT-4 when first released, and still holds up well ~6 months later (which is a long time for LLMs!). One notable aspect of the model is its range of sizes available - from 0.5B to 1.5B, all the way to 72B, all variants perform well for their class. The model performs especially well on math and code, and has been further fine-tuned for those domains with its variants, Qwen-2-Math and Qwen-2.5-Coder.

The first two phases of their training process - pretraining and SFT - are fairly standard. The third phase, RLHF, introduces some novel techniques:

1. They first trained a reward model from their initial unaligned language model.
2. Then, they use that reward model to score N completions from their policy model. This forms completion pairs.
3. Those completion pairs are used to align the model via DPO. This is performed iteratively, so every N steps, re-sample the model, rank the completions and continue.

This technique is similar to the Llama 3 approach, but the Qwen authors mention that they also use an Online Merging Optimizer to "mitigate the alignment tax" during their post-training process².

So what is the alignment tax and OMO? The alignment tax is a phenomenon where performing RLHF can cause the model to forget information learned during pretraining or SFT. For example, a model might be able to complete a coding problem after pretraining, but after RLHF, it can't, even when prompted with a chat template; the theory is that the model has learned such totally different biases in order to maximize reward during RLHF that its attention patterns shift, losing some information learned during pretraining.

A common solution to this is model averaging, where multiple RLHF steps are performed with different data mixtures, then merged together with a solution like TIES to produce a final model. Similarly, a popular method in the community is what I'll call Rombodawg's method:

1. Fine-tune the base model on the intended dataset with LoRA.
2. Apply the LoRA onto the instruct model.
3. Merge all three - the instruct model, the fine-tuned instruct model, and the base model - with TIES using MergeKit.

However, these approaches have their downsides. Model averaging requires training N models, which increases costs by an equivalent amount. As for Rombodawg's method, I've personally had mixed results with it, sometimes due to the LoRA failing to capture enough of the format or information I want to train into the model. OMO takes the model merging approach and applies a similar method during training, implementing it within the optimizer. The idea is to make the gradient at each step represent the optimal tradeoff between the base model parameters and the human-preference parameters. The function used to determine this is:

$$\theta^{(t+1)} = \theta_b + \mathcal{F} \left( \tau^{(t)} + \Delta \theta^{(t)} \right) \oplus \mathcal{F} \left( \tau_r \right)$$

This can be broken down into the following process:

1. Add the gradients, $\Delta \theta^{(t)}$, to the policy model, $\tau^{(t)}$, and sparsify the result ($\mathcal{F}$ is the sparsification operator, which can be TIES, top-K, or another method).
2. Sum the reference model with the policy model.
3. Apply a consensus operation, $\oplus$, between the left-hand side and the sparsified SFT model, $\tau_r$. The consensus operation can be any merging method, from summation, averaging, TIES, DARE, or any other.

As you can see, this is similar to the process done offline during model merging, but performed at each training step. While it does require more time and memory (and compute) on each step, this avoids the need to align multiple independent variants and merge them offline. The paper demonstrates better results on several benchmarks than offline merging. The OMO repo provides implementations of a few common optimizers, like Adam, with OMO capabilities.

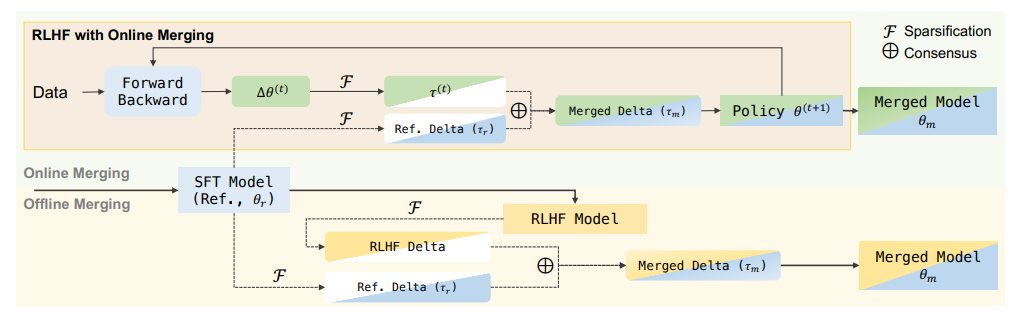An illustration of OMO applied to a standard RLHF pipeline, figure 1 in the paper.

I'm excited to try these techniques in my next set of LLM experiments; reach out if you found this article helpful or are interested in these techniques!

Footnotes

1. With the exception of OMO, which has a paper dedicated to it. ↩

2. Llama 3 mentions using multiple rounds of model merging, which likely performs the same function. ↩