Tricks for DPO tuning a Code LLM, Part 1 - Logit Curriculum Learning

Background

I've been experimenting with different techniques for fine-tuning LLMs to improve on code generation tasks, as I find it an interesting domain for testing alignment techniques for a few reasons:

• In many cases, there's clear ground truth in the form of execution feedback or unit test results; in other words, it's a crisp task which means it fits well with many different forms of reinforcement learning. In fact, some papers simply use the no. of tests completed as the reward function.
• Code generation is also something that LLMs currently excel at, relative to other tasks; it's likely the largest single-domain driver of revenue in the space.
• There's a clear path from single-step code generation to multi-step agentic workflows.

However, the piece that's still under heavy development is the post-training or alignment piece. While reward models, and RLCEF models exist, they're expensive to train and often unstable; so I've been exploring the possibility of using preference models like DPO instead.

In this series, I'll explore a few different techniques that can be used to improve the quality of DPO alignment for coding. I'll start with a baseline, add techniques one by one, and see how this improves performance on a few common benchmarks.

The plan

Dataset

For DPO tuning, a dataset is required to contain the following fields:

• Prompt
• Rejected completion.
• Accepted completion.

Following the CodeLLM-DPO paper, I used best-of-N sampling with a prompt subset from the CodeContests dataset, using the model I planned to tune, to ensure completions are on-policy. I wrote a framework that evaluates the code against a series of provided unit tests; the highest-scoring sample is used as the accepted completion, the lowest-scoring sample as the rejected completion.

Model

I decide to use LLama 3.1 8B as the base model for these experiments; I wanted to choose something that would be non-cost-prohibitive for others to test, but would also contain enough built-in reasoning ability to allow it to perform decently well on standard benchmarks like MBPP and HumanEval.

Evaluation

I decided to stick with MBPP and HumanEval, which are the most common basic evals for code completion. Since both evals are Python-only, I decided to restrict the tuning to Python-only as well.

A note on interpereters

A lot of implementations of HumanEval and similar evals use the python.exec() function to interperet and execute the LLM-generated code as part of execution. While this is very easy to implement, there are a few obvious downsides:

• Safety; unless proper sandboxing is done, the LLM has access to whatever system is executing the code.
• Thread-safety / performance; this approach requires spinning up a process per test, which can get really expensive, especially when running hundreds of concurrent tests.

Instead, I decided to take a page from the HuggingFace Transformers library's approach to tool use: writing a simple interpereter that takes the output of Python's ast.parse and evaluating it inline. This executed significantly faster, as I could re-use the same processes for all tests; and I could be sure that no code outside of a restricted set of modules would be executed.

Curriculum learning

Once I had an initial dataset in DPO format, I ran an initial training run with the dataset as-is. While the initial bump was decent, I noticed that some pairs seemed significantly more divergent than others; certain positive-negative pairs only different in syntax or edge case handling, while others contained radically different approaches to solving the problem.

This made me wonder if the relative differences might lead to losses that are too high, adding nuance the model might not know yet, which points to curriculum learning as a potential solution: starting with the 'easiest' samples, gradually introduce harder and harder samples. While ReflectionCoder performs curriculum learning on multiple samples from the same problems, using dynamic masking, I wondered if I could instead just use the difference in logits instead.

Details

The DPO loss gradient is as follows:

$$\left[ \sigma\left(\hat{r}\theta(x, y_l) - \hat{r}\theta(x, y_w)\right) \cdot \left( \nabla_\theta \log \pi_\theta(y_w \mid x) - \nabla_\theta \log \pi_\theta(y_l \mid x) \right) \right]$$

Which, assuming $r_0 = \hat{r}\theta(x, y_l)$, means the per-token logprob distance is all that's needed to determine the loss. Applying that against the dataset gives us the following results:

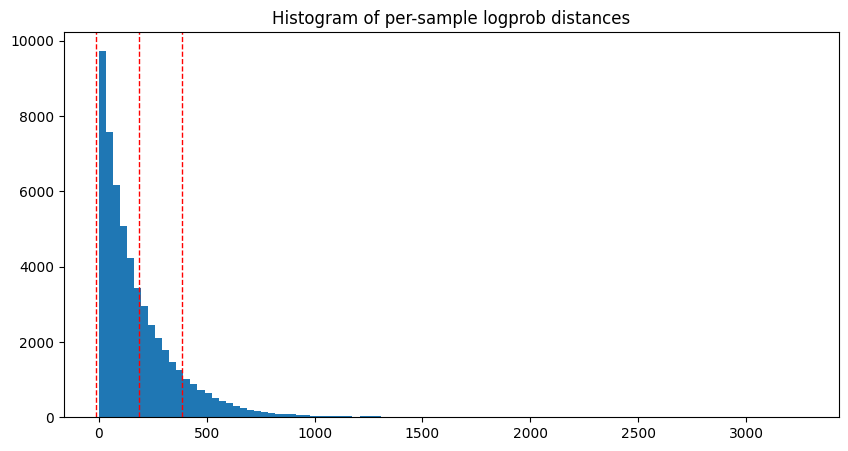
I then split the dataset by 10th percentile, 50th percentile, and 90th percentile logprobs distance. A quick review of samples showed that this generally maps well to the difference in results.

Example 1: High logprobs distance (90th percentile)

Rejected

def min_different_letters(a, b, l, r):
    # Calculate the total number of moves made by both players
    total_moves = (r + b - 1) // b  # Total moves until position r
    total_length = total_moves * b + (total_moves - 1) * a  # Length of the string after > total_moves
    
    # Calculate the number of distinct letters in the segment
    # The maximum number of distinct letters is limited by `a`
    # The minimum number of distinct letters is determined by the overlap of moves
    if total_length < l:
        return 0  # If the segment is out of bounds, return 0
    
    # The number of distinct letters can be calculated based on the number of moves
    # Mister B moves first, so he can control the letters in the first b positions
    # The opponent will then add a letters, and this pattern continues
    
    # The number of distinct letters in the segment can be calculated as follows:
    # Each complete cycle of moves contributes a distinct set of letters
    # The number of complete cycles that fit in the range [l, r]
    
    # Calculate the number of complete cycles in the range
    start_cycle = (l - 1) // (b + a)
    end_cycle = (r - 1) // (b + a)
    
    # The number of distinct letters in the segment can be calculated
    distinct_letters = set()
    
    # Add letters from Mister B's moves
    for cycle in range(start_cycle, end_cycle + 1):
        for i in range(b):
            letter = chr((cycle * (b + a) + i) % a + ord('a'))
            distinct_letters.add(letter)
        
        # Add letters from the opponent's moves
        for j in range(a):
            letter = chr((cycle * (b + a) + b + j) % a + ord('a'))
            distinct_letters.add(letter)
    
    return len(distinct_letters)

# Read input
a, b, l, r = map(int, input().split())
# Get the result
result = min_different_letters(a, b, l, r)
# Print the result
print(result)

Accepted

def min_different_letters(a, b, l, r):
    # Calculate the number of turns for both players
    total_moves = (r - 1) // (b + a) + 1
    letters_in_segment = set()
    
    # Determine the letters added by Mister B
    for i in range(total_moves):
        # Mister B's turn
        letters_in_segment.update(chr((i % a) + ord('a')) for j in range(b))
        
        # Opponent's turn
        if i < total_moves - 1 or (r - 1) % (b + a) >= b:
            letters_in_segment.update(chr((i % a) + ord('a')) for j in range(a))
    
    # The minimum number of different letters in the segment from l to r
    return len(letters_in_segment)

# Read input
a, b, l, r = map(int, input().split())
# Output the result
print(min_different_letters(a, b, l, r))

Example 2: Low logprobs distance (10th percentile)

Rejected

def max_beauty_journey(n, beauties):
    dp = [0] * n
    dp[0] = beauties[0]
    
    for i in range(1, n):
        dp[i] = beauties[i]
        for j in range(i):
            if i - j == beauties[i] - beauties[j]:
                dp[i] = max(dp[i], dp[j] + beauties[i])
    
    return max(dp)

# Read input
n = int(input())
beauties = list(map(int, input().split()))

# Get the result
result = max_beauty_journey(n, beauties)
print(result)
def max_beauty_journey(n, beauties):
    dp = [0] * n
    dp[0] = beauties[0]
    
    for i in range(1, n):
        dp[i] = beauties[i]
        for j in range(i):
            if i - j == beauties[i] - beauties[j]:
                dp[i] = max(dp[i], dp[j] + beauties[i])
    
    return max(dp)

# Example usage
n1 = 6
beauties1 = [10, 7, 1, 9, 10, 15]
print(max_beauty_journey(n1, beauties1))  # Output: 26

n2 = 1
beauties2 = [400000]
print(max_beauty_journey(n2, beauties2))  # Output: 400000

n3 = 7
beauties3 = [8, 9, 26, 11, 12, 29, 14]
print(max_beauty_journey(n3, beauties3))  # Output: 55

Accepted

def max_beauty_journey(n, beauties):
    dp = [0] * n
    dp[0] = beauties[0]
    
    for i in range(1, n):
        dp[i] = beauties[i]
        for j in range(i):
            if i - j == beauties[i] - beauties[j]:
                dp[i] = max(dp[i], dp[j] + beauties[i])
    
    return max(dp)

• The failed completions tend to have lots of example cases and comments, while the successful completions tend to be more concise. Something to look into more; maybe the model becomes overly confident when it sees a sample similar to one with lots of unit tests.
• I haven't run into the dreaded DPO over-verbosity issue yet, but I would imagine it would be a problem with longer completions, as the average length distance between the two completions increases.

There are a few other options for filtering that might work, such as:

• AST distance between winning / losing completion
• Test pass count distance between winning / losing completion

However, I decided to save those for future exploration as those don't generalize well to non-coding tasks.

Results

I performed evaluation with MBPP and HumanEval after each part of the curriculum, and compared to the same step count for a randomly shuffled version of the same dataset.

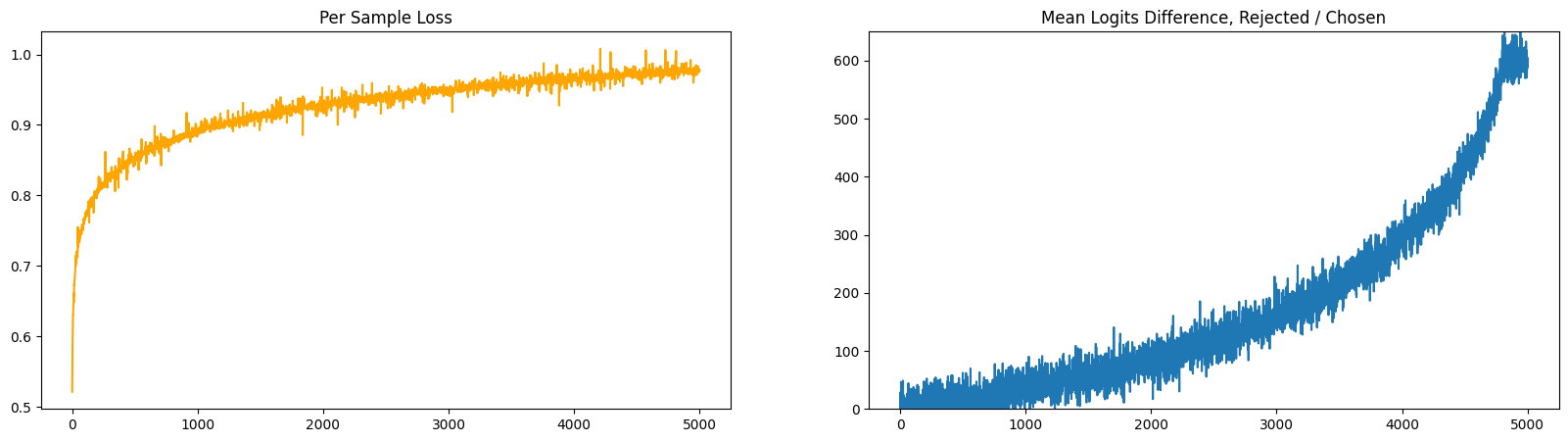
Below is a comparison of the loss recorded per-sample for a single epoch, vs the logit distance between the winning and losing completions.

And here are the benchmark results:

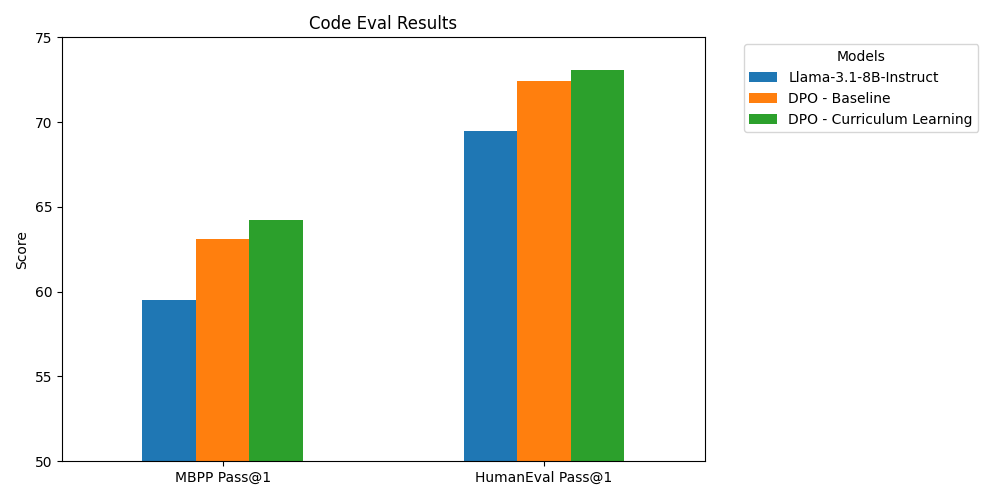
As you can see, this improves performance on the two benchmarks relative to shuffling. More work is required to see if this transfers to a larger dataset or model, but it's a promising start.

Failure cases / things to watch out for

• I noticed that many of the samples in the 10th percentile were simply incorrect completions; this is likely due to the fact that the model is not yet able to generalize to the edge cases in the dataset. I decided to manually prune these completions.
• I also removed a certain number of samples in the 90th percentile that simply added more comments to the code; while this is a valid completion, it doesn't seem to improve the model's performance, and could lead to the model being over-verbose with comments.
• Interestingly, similar to the DeepSeekMath paper's findings, there are a certain number of samples that simply weren't solvable, even with continued tuning; the number of tests passed continued to rise on the same problems, but others simply weren't passing. I didn't see anything obviously different with these samples, but more analysis is needed.

Conclusion

I'm still working on cleaning up the codebase and dataset, but I'll be publishing them, along with the model checkpoints and eval results, in the next few weeks.

If you are working on similar problems, please reach out via email here, I'd love to chat!