Training a Reasoning Model for Very Cheap with DPO

Reasoning is the talk of the town - if the 'town' in question is AI Twitter - and has been since OpenAI's announcement of O1 in late 2024. A number of similar 'reasoning' models have followed, some open, like Qwen's QWQ, and some propietary, like DeepSeek's R1 and Google's Gemini Flash Thinking; however, as is often the case with LLM releases these days, little research has been published from each of these groups on how exactly these reasoning models are trained. What we do know is that these models are expensive and difficult to train, requiring the kinds of resources that are rare outside of large labs; distributed PPO-based RLHF is already prohibitively expensive and complex, owing to requiring a large number of distinct operations and model sync points during training, so you can imagine the difficulty in scaling that to the amount of data and compute required to train a reasoning model.

The other talk of the town, specific in LLM post-training (and to a lesser, but still notable extent, diffusion models) is DPO, or Direct Preference Optimization. There are lots of great guides out there on DPO so I won't repeat them, but DPO is significantly easier to both run - since it simply requires two forward passes of a single model - and to generate data for, since it can be generated offline. For many tasks, especially basic alignment for chatbot-lke behavior, DPO works just as well as RLHF¹, and is much cheaper to run.

So, if you combine these two ideas - DPO and reasoning / chain of thought - you get an obvious candidate for a LLM post-training paper in the year 2024, and indeed many (at least two dozen, in my notes) have been published on this topic. The value proposition is clear: once you find an approach that works, in theory you could train a reasoning model for a fraction of the cost of the current state of the art, therefore democratizing the ability to develop and improve them. Thinking a little more cynically - this also lets researchers without the resources of the big labs participate in the Current Thing in AI.

In this post I'll review a few of the most interesting papers on this topic, and discuss some of the common themes and approaches that have emerged. I've also been experimenting with training a reasoning model using DPO myself, and in the near future I'll shre more details on the approach I've used - which is a combination of the techniques outlined below.

Step-Controlled DPO

The most common formulation of DPO for reasoning goes like this:

1. SFT tune a LLM to perform chain-of-thought, or discrete reasoning steps, to solve problems in a specific domain.
2. Generate N completions for a set of problems in that domain.
3. Verify the outputs using an external ground truth verifier (such as unit tests or a calculator for math problems). Choose an accepted and rejected (i.e. good and bad) completion from that set, and use that as the basis for the DPO tuning.

While this does work, and can provide better results than just SFT tuning, clearly there are some limitations. One is that there's a chance the reasoning steps might be wrong, but the completion is still correct; another is that DPO might unintentionally move the model towards incorrect reasoning, or might not be able to assign credit to the specific tokens that improve reasoning abilities.

These are the problems that Step-Controlled PPO aims to fix. I liked this paper because it applies a few minimal changes to the above approach, and demonstrates some minimal but tangible improvements. The codebase and dataset used are also available, which is always great to see. The techniques are as follows:

1. First, they performed SFT on a specific format of CoT, to ensure it can generate the syntax required easily. This also means the model doesn't have to learn the syntax during the DPO phase. This dataset is generated with temperature=1 so it has the highest likelihood of being correct. It is then filtered so only correct chains (with correct steps) are used.
2. Then, they take that SFT dataset of step-wise reasoning chains, and randomly drop out all steps past a certain random step number. Once this is done, they gradually increase the temperature while generating individual steps, so that the likelihood of a bad output is greater.
   • For example, if step 4 is dropped out, step 5 is generated with temperature=1.05, step 6 with temperature=1.1, and so on.
3. They then use a ground truth verifier to verify the correctness of each step, and use the accepted and rejected steps as the basis for DPO tuning.

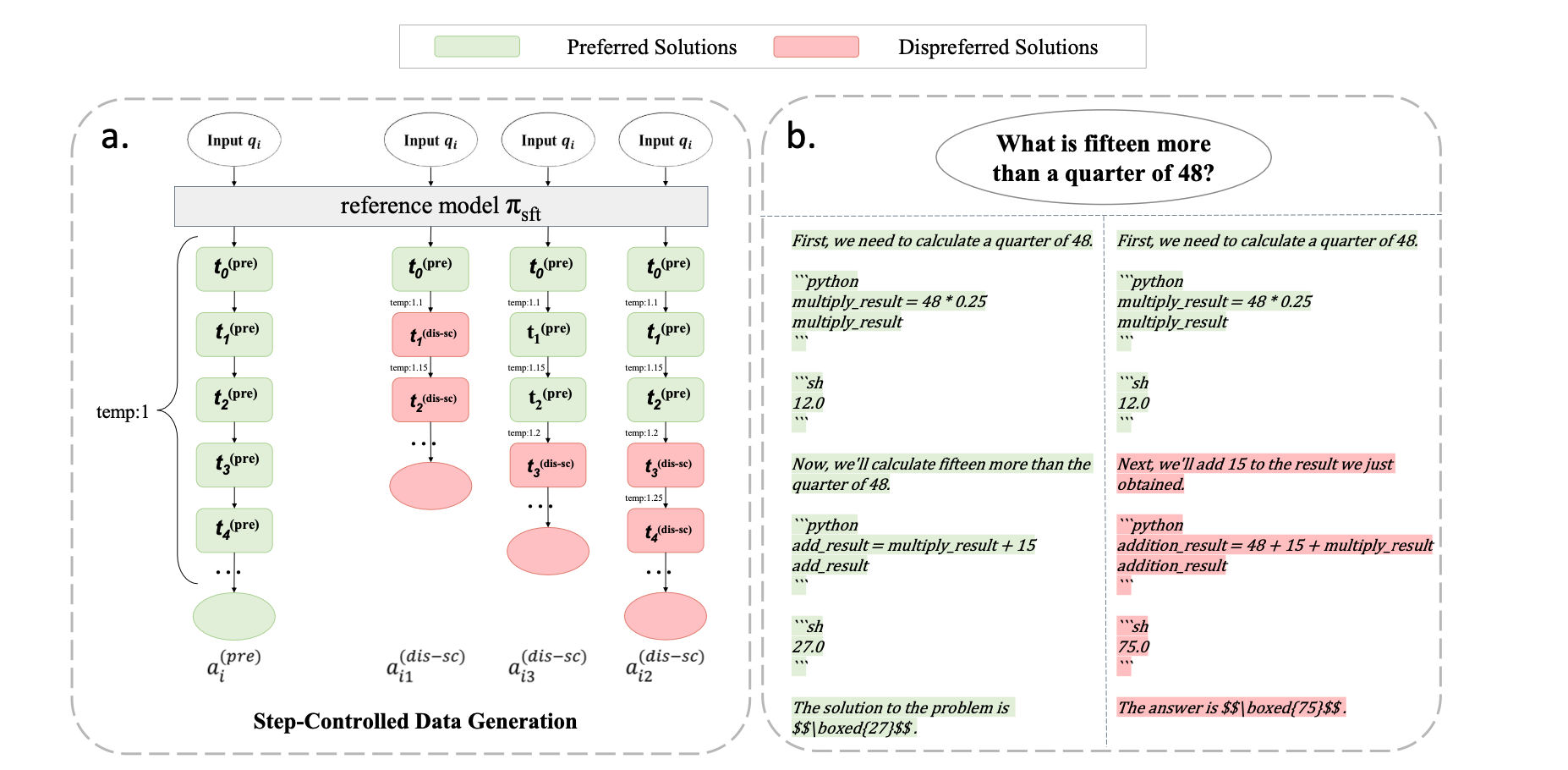Figure 1 in the paper, showing the overall process of generating the DPO dataset.

Given that you can then randomly sample a N * S different steps to drop out, this can lead to a pretty large dataset. The authors show that this can result in a more robust model, and that the model can generalize to new reasoning chains better than the SFT-only model. Interestingly, the model trained in this approach also demonstrates better credit assignment; the log-probability of incorrect tokens in evaluated completions is much lower than in the SFT-only model.

Figure 3 in the paper. Note that the incorrect equation - 8 + 1 + 1 \mod 9 - has a much lower log-probability in StepDPO (left) than standard DPO (right).

Step DPO

Paper

While this paper has an extremely similar name to the last, it's not related. The problems they aim to solve are similar, however, namely DPO's issues with credit assignment, as well as the tendendcy for DPO to increase the model's likelihood of generating incorrect completions as well as correct ones. The authors propose a step-wise DPO approach that aims to solve these problems.

The approach is as follows:

1. SFT tune an LLM to perform chain-of-thought, or discrete reasoning steps, to solve problems in a specific domain. This is done with ~300k samples.
2. Generate N completions and select a preferred correct completion, and an incorrect completion, for each problem.
3. Perform step-wise DPO tuning. This follows the below formulation:

$\mathcal{L}(\theta) = - \mathbb{E}_{(x, s_1 \sim k-1, s_\text{win}, s_\text{lose}) \sim D} \Bigg[\log \sigma \Bigg( \beta \log \frac{\pi_\theta(s_\text{win} \mid x; s_1 \sim k-1)}{\pi_\text{ref}(s_\text{win} \mid x; s_1 \sim k-1)} - \beta \log \frac{\pi_\theta(s_\text{lose} \mid x; s_1 \sim k-1)}{\pi_\text{ref}(s_\text{lose} \mid x; s_1 \sim k-1)} \Bigg) \Bigg]$

Which is effectively the DPO loss function but formulated for individual steps. The steps to train on are randomly sampled, and all others are masked out. In theory, this leads to better credit assignment.

The paper shows a modest improvement over the base models it uses, and over a DPO-tuned model; however, since this and the above paper use different base models it's hard to directly compare the tuning method. Would be nice if model choices were slightly more standardized for post-training research.

Your Language Model is Secretly a Reward Model

Paper

While this paper isn't directly related to code generation, I found it to be really valuable when thinking about DPO for reasoning. It connects DPO to Q-learning in a way that allows us to model the DPO loss as a token-level MDP, which means that DPO is learning credit assignment to some degree; it simply performs worse than PPO in many cases, but theoretically, the authors argue, there's no fundamental reason why can't meet or exceed other Q-learning based optimization aproaches.

The paper also formulates a token-level DPO function, by treating the tokens as a MDP, and DPO as a solution to the Bellman equation. Further, the authors state that DPO is always fitting an optimal advantage for some implicit reward, generally the reward provided by human preference; however, if you replace human preference with a reward model that determines preference, then this is equivalent to PPO or any other Q-learning based approach.

This connection then opens the door to applying DPO to a number of techniques in RL that make use of search, such as Monte Carlo Tree Search. Using this token-level formulation, we can treat each token as a state, and perform a tree search by decoding tokens in a beam search-like fashion, and then using the DPO loss to determine the best path through the tree.

Additionally, the authors demonstrate that the average reward should decrease over time, given that the KL divergence of samples should be positive; the implication here is that we want to SFT tune the model first, so that the average reward is higher, and then apply DPO to fine-tune the model to a lower average reward, which should lead to better generalization.

There are not a lot of concrete practical takeaways from this paper, but it raises some interesting questions about the pipeline of SFT->DPO, and how to perform exploration for DPO dataset curation. Specifically, since reading this paper I've switched from splitting my datasets into SFT and DPO splits, and instead perform SFT and DPO on the same dataset, which has led to better results in my experiments. I'm also interested in exploring the MCTS approach to DPO, and how it might be applied to reasoning tasks.

Figure in the paper, showing DPO loss applied to a summarization task. On the left is the correct response, and on the right, incorrect statements are introduced; DPO correctly gives a higher loss to the tokens that are incorrect.

Footnotes

1. See the Zephyr project by HuggingFace. ↩